Advertisements
Advertisements
प्रश्न
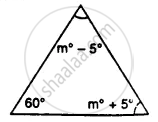
Find the unknown marked angles in the given figure:
उत्तर
In the figure,
∠A + ∠B + ∠C = 180° .....(Sum of angles of a triangle)
(m°− 5°) + 60° + (m°+ 5°) = 180°
⇒ m°− 5° + 60° + m° + 5° = 180°
⇒ 2m° = 180°− 65° + 5°
⇒ 2m° = 120°
⇒ ∴ m° = `(120°)/2=60°`
Hence ∠A = m°− 5° = 60°− 5° = 55°
and ∠C = m° + 5° = 60° + 5° = 65°
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Can a triangle have two right angles? Justify your answer in case.
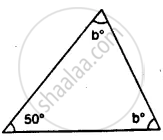
Find the unknown marked angles in the given figure:
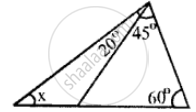
In the following, find the marked unknown angle:
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.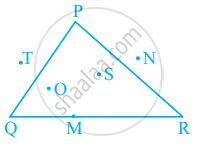
Which two triangles have ∠B in common?