Advertisements
Advertisements
प्रश्न
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
पर्याय
Ture
False
उत्तर
If one angle of a triangle is obtuse, then it cannot be a right angles triangle.
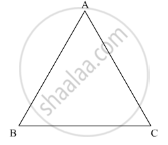
According to the angle sum property of the triangle
In ΔABC
∠A +∠B + ∠C = 180°
Now, if it is a right angled triangle
Then,
∠A + ∠B + ∠C = 180°
90° + ∠B + ∠C =180°
∠B +∠C = 90°
Also if one of the angle’s is obtuse
∠B +∠C > 90°
This is not possible.
Thus, if one angle of a triangle is obtuse, then it cannot be a right angled triangle.
APPEARS IN
संबंधित प्रश्न
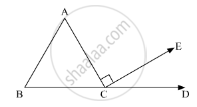
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
Can a triangle together have the following angles?
33°, 74° and 73°
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
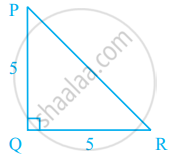
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is ______.