Advertisements
Advertisements
प्रश्न
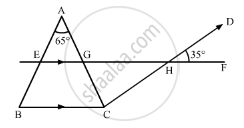
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
उत्तर
In the given figure,,AB || CD,EF || BC ∠BAC = 65° and ∠DHF = 35°
We need to find ∠AGH
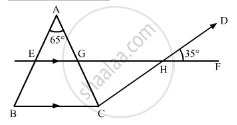
Here, GF and CD are straight lines intersecting at point H, so using the property, “vertically opposite angles are equal”, we get,
∠DHF = ∠GHC
∠GHC = 35°
Further, as AB || CD and AC is the transversal
Using the property, “alternate interior angles are equal”
∠BAC = ∠ACD
∠ACD = 65°
Further applying angle sum property of the triangle
In ΔGHC
∠GHC + ∠HCG + CGH = 180°
∠CGH + 35° + 65° = 180°
100 + ∠CGH = 180°
∠CGH = 180°- 100°
∠CGH = 80°
Hence, applying the property, “angles forming a linear pair are supplementary”
As AGC is a straight line
∠CGH + ∠AGH = 180°
∠AGH + 80° = 180°
∠AGH + 180° - 80°
∠AGH = 100°
Therefore, ∠AGH = 100°
APPEARS IN
संबंधित प्रश्न
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Can a triangle have two obtuse angles? Justify your answer in case.
Can a triangle have All angles more than 60°? Justify your answer in case.
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
Define a triangle.
In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
Find the unknown marked angles in the given figure:
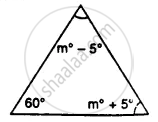
In a ∆ABC, AB = AC. The value of x is ________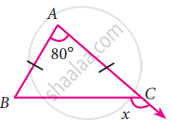
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
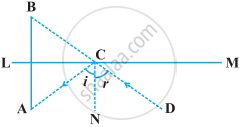
Which two triangles have ∠B in common?