Advertisements
Advertisements
प्रश्न
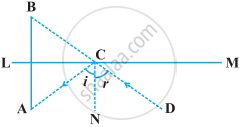
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
उत्तर १
Given: An object OA placed at a point A, LM be a plane mirror, D be an observer and OB is the image.
To prove: The image is as far behind the mirror as the object is in front of the mirror i.e., OB = OA.
Proof: CN ⊥ LM and AB ⊥ LM
⇒ AB || CN
∠A = ∠i [Alternate interior angles] ...(i)
∠B = ∠r [Corresponding angles] ...(ii)
Also, ∠i = ∠r [∵ incident angle = reflected angle] ...(iii)
From equations (i), (ii) and (iii),
∠A = ∠B
In ΔCOB and ΔCOA,
∠B = ∠A ...[Proved above]
∠1 = ∠2 ...[Each 90°]
And CO = CO ...[Common side]
∴ ΔCOB ≅ ΔCOA ...[By AAS congruence rule]
⇒ OB = OA ...[By CPCT]
Hence proved.
उत्तर २
In ΔOBC and ΔOAC,
∠1 = ∠2 ...[Each 90°]
Also, ∠i = ∠r [∵ incident angle = reflected angle] ...(i)
On multiplying both sides of equation (i) by –1 and then adding 90° both sides, we get
90° – ∠i = 90° – ∠r
⇒ ∠ACO = ∠BCO
And OC = OC ...[Common side]
∴ ΔOBC ≅ ΔOAC ...[By ASA congruence rule]
⇒ OB = OA ...[By CPCT]
Hence, the image is as far behind the mirror as the object is in front of the mirror.
APPEARS IN
संबंधित प्रश्न
In ΔABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
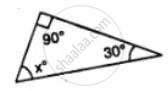
Find the unknown marked angles in the given figure:
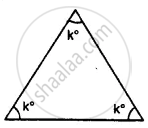
Calculate the unknown marked angles of the following figure :
Classify the following triangle according to sides:
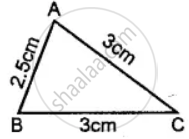
Classify the following triangle according to sides:
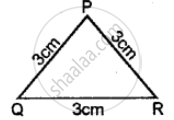
In a ∆ABC, AB = AC. The value of x is ________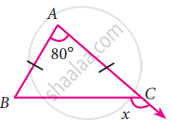
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.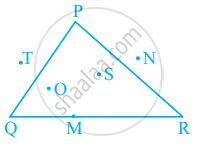
Can we have two acute angles whose sum is a straight angle? Why or why not?
