Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
उत्तर
∠A + ∠B + ∠C= 180°
⇒ 62° + 62° + ∠C = 180°
⇒ 124° + ∠C = 180°
⇒ ∠C = 180° – 124°
⇒∠C = 56°
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
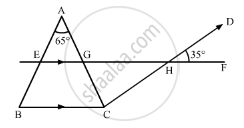
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
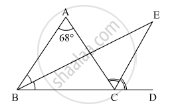
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
If two sides of a triangle are 5 cm and 1.5 cm, the length of its third side cannot be ______.
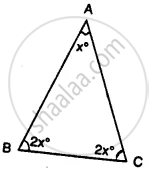
Find the value of the angle in the given figure:
The correct statement out of the following is 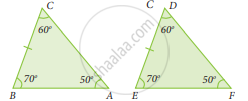
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
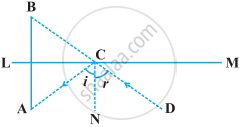
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
