Advertisements
Advertisements
प्रश्न
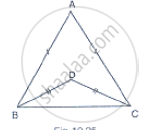
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Advertisements
उत्तर
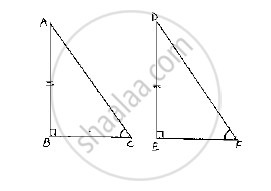
Given that, in two right triangles one side and acute angle of one are equal to the corresponding side and angle of the other
We have to prove that the triangles are congruent
Let us consider two right triangles such that
∠B=∠E=90° .................(1)
AB=DE ..................(2)
∠C=∠F ..................(3)
Now observe the two triangles ABC and DEF
∠C=∠F [From (3)]
∠B=∠E [From (4)]
and AB =DE [From (2)]
So, by AAS congruence criterion, we have
ΔABC≅ΔDEF
∴ The two triangles are congruent
Hence proved
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
- OB = OC
- AO bisects ∠A
Show that the angles of an equilateral triangle are 60° each.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
The vertical angle of an isosceles triangle is 100°. Find its base angles.
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
In a ΔABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Prove that each angle of an equilateral triangle is 60°.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
In the given figure, what is y in terms of x?
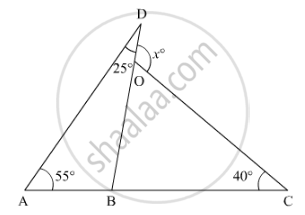
In the given figure, the value of x is ______.
In the given figure, if BP || CQ and AC = BC, then the measure of x is
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
