Advertisements
Advertisements
प्रश्न
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
पर्याय
25°
30°
45°
60°
उत्तर
In the given figure, measures of the angles of ΔABC are in the ratio 3 : 4 : 5. We need to find the measure of the smallest angle of the triangle.
Let us take,
∠A = 3x
∠B = 4x
∠C = 5x
Now, applying angle sum property of the triangle in ΔABC, we get,
∠A + ∠B + ∠C = 180°
3x + 4x + 5x = 180°
12X = 180°
`x = (180°)/ 12`
x = 15°
Substituting the value of x in ,∠A,∠Band∠C
∠A = 3(15°) = 45
∠B = 4(15V) = 60
∠C = 5(15°) = 75°
Since, the measure of ∠A is the smallest
Thus, the measure of the smallest angle of the triangle is 45°
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
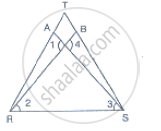
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT
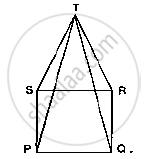
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
In the given figure, if EC || AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is
Which of the following correctly describes the given triangle?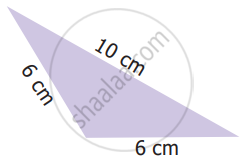
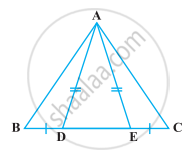
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
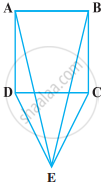
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
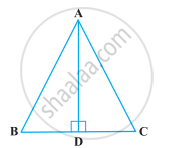
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
