Advertisements
Advertisements
प्रश्न
Classify the following triangle according to angle:
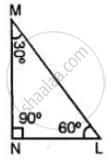
उत्तर
Since ∠MNL = 90°, and sum of two acute angle ∠M + ∠N = 30° + 60° = 90°. Hence, it is a right angled triangle.
APPEARS IN
संबंधित प्रश्न
If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right triangle.
Can a triangle have two acute angles?Justify your answer in case.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
8.4 cm, 16.4 cm, 4.9 cm
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
