Advertisements
Advertisements
प्रश्न
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
उत्तर
In Δ ABC,

∵ AB = AC.
∴ ∠B = ∠C
But ∠A = 100°
and ∠A + ∠B + ∠C = 180° ..........(Angles of a triangle)
⇒ 100° + ∠B + ∠B = 180°
⇒ 2 ∠B = 180°− 100°
⇒ 2 ∠B = 80°
∴ ∠B =`(80°)/2=40°`
Hence ∠B = ∠C = 40°
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are arranged in ascending order of magnitude. If the difference
between two consecutive angles is 10°, find the three angles.
Can a triangle have two obtuse angles? Justify your answer in case.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

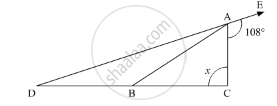
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
If two acute angles of a right triangle are equal, then each acute is equal to
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
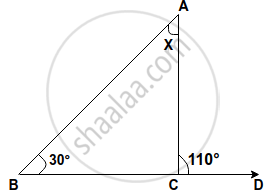
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
Classify the following triangle according to sides: