Advertisements
Advertisements
Question
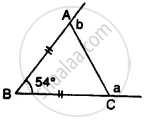
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.
Solution
In Δ ABC, sides BA and BC are produced
∠ABC = 54°; AB = BC
Now in Δ ABC,
∠BAC + ∠BCA + ∠ABC = 180° ...........(Angles of a triangle)
⇒ ∠BAC + ∠BAC + 54° = 180° .............(∵ AB = BC)
⇒ 2 ∠BAC = 180° − 54°
⇒ 2 ∠BAC = 126°
∴ ∠BAC =`(126°)/2=63°` and ∠BCA = 63°
∠BAC + b = 180° ..............(Linear pair)
⇒ 63° + b = 180°
⇒ b = 180° − 63° = 117°
and ∠BCA + a = 180° ............(Linear pair)
∴ 63° + a = 180°
⇒ a = 180° − 63° = 117°
Hence a = 117°, b = 117
APPEARS IN
RELATED QUESTIONS
Find the unknown angles in the given figure:
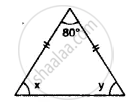
Find the unknown angles in the given figure:
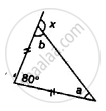
Find the unknown angles in the given figure:
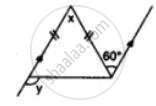
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
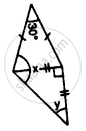
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
In the given figure, BI is the bisector of ∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.
In Figure, BP bisects ∠ABC and AB = AC. Find x.
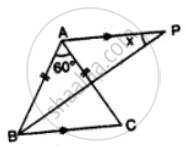
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠ABE

In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠BAE
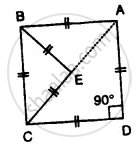
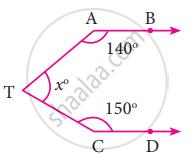
In the figure, AB is parallel to CD, find x