Advertisements
Advertisements
Question
Construct a ∆ ABC such that AB = 6 cm, BC = 4.5 cm and AC = 5.5 cm. Construct a circumcircle of this triangle.
Solution
Steps of Construction :
(i) Draw a line segment BC = 4.5 cm
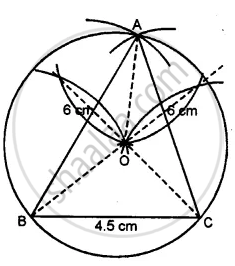
(ii) With centre B and radius 6 cm, draw are arc
(iii) With centre C and radius 5.5 cm, draw another arc intersecting the first arc at A.
(iv) Join AB and AC.
Δ ABC is the required triangle.
(v) Draw the perpendicular bisectors of AB and AC. Which intersects each other at O.
(vi) Join OB, OC and OA.
(vii) With centre O and radius OA, draw a circle which passes through A, B and C.
This is the required circumcircle of Δ ABC.
APPEARS IN
RELATED QUESTIONS
Construct a ∆ ABC such that:
BC = 6 cm, AC = 5.7 cm and ∠ACB = 75°
Construct a ∆ ABC such that:
AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Construct a ∆ PQR such that :
PQ = 6 cm, ∠Q = 60° and ∠P = 45°. Measure ∠R.
Construct a ∆ PQR such that:
QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
Construct an isosceles Δ ABC such that:
Base BC = 4 cm and base angle = 30°. Measure the other two sides of the triangle.
Construct an isosceles Δ ABC such that:
Base AB = 6.2 cm and base angle = 45°. Measure the other two sides of the triangle.
Construct an isosceles ∆ ABC such that:
AB = AC = 6.5 cm and ∠A = 60°
Construct an isosceles ∆ ABC such that:
BC = AB = 5.8 cm and ZB = 30°. Measure ∠A and ∠C.
Construct an equilateral Δ ABC such that:
AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB, and PC.
Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
