Advertisements
Advertisements
Question
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
Solution
Let each angle of the base of the isosceles triangle = x°
Then vertical angle = x + 15°
Now x + x + x + 15° = 180° ............(Sum of angles of a triangle)
⇒ 3x + 15°= 180°
⇒ 3x = 180° − 15° = 165°
⇒ x =`(165°)/3=55°`
Hence each base angle = 55°
and vertical angle = 55° + 15° = 70°
APPEARS IN
RELATED QUESTIONS
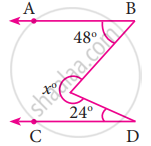
Find the unknown angles in the given figure:
Find the unknown angles in the given figure:
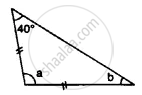
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
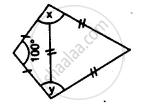
Find the unknown angles in the given figure:
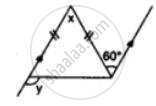
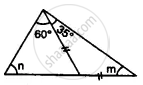
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
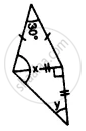
In an isosceles triangle, each base angle is four times its vertical angle. Find all the angles of the triangle.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
In the given figure, BI is the bisector of ∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.
Find x in Figure Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.
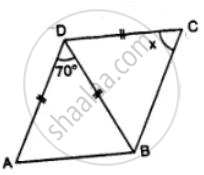
In the figure, AB is parallel to CD, find x