Advertisements
Advertisements
प्रश्न
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.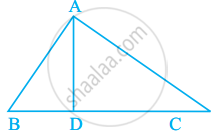
पर्याय
1
2
3
4
उत्तर
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is 3.
Explanation:
A triangle, in which one angle is equal to 90° is called a right-angled triangle.
Since, ∠BAC = 90°
ΔBAC is a right-angled triangle.
Also, ∠ADB = ∠ADC = 90° ......[ AD Perpendicular to BC]
∠ADB and ∠ADC are also right-angled triangles.
Hence, there are 3 right-angled triangles.
APPEARS IN
संबंधित प्रश्न
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
Can a triangle have two acute angles?Justify your answer in case.
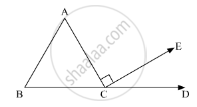
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
Find, giving a reason, the unknown marked angles, in a triangle drawn below:

Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
Can we have two acute angles whose sum is a straight angle? Why or why not?
