Advertisements
Advertisements
Question
If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is
Options
90°
180°
270°
360°
Solution
n the given ΔABC, all the three sides of the triangle are produced. We need to find the sum of the three exterior angles so produced.
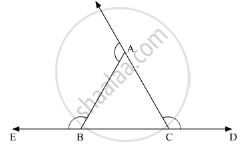
Now, according to the angle sum property of the triangle
∠A + ∠B + ∠C = 180° .......(1)
Further, using the property, “an exterior angle of the triangle is equal to the sum of two opposite interior angles”, we get,
ext.∠C = ∠A + ∠B ......(2)
Similarly,
ext.∠A = ∠C + ∠B .......(3)
Also,
ext.∠B = ∠C+ ∠A .......(4)
Adding (2) (3) and (4)
We get,
ext.∠A + ext.∠B+ ext.∠C = ∠C+∠B +∠C +∠A + ∠B + ∠A
= 2(∠A= ∠B+ ∠C )
= 2 (180°)
= 360°
Thus, ext. ∠A + ext. ∠B ext.∠C = 360°
APPEARS IN
RELATED QUESTIONS
Can a triangle have All angles more than 60°? Justify your answer in case.
Can a triangle have All angles less than 60° Justify your answer in case.
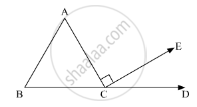
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
Fill in the blank to make the following statement true:
An exterior angle of a triangle is always ......... than either of the interior opposite angles.
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
The angles of a triangle are in the ratio 2 : 3 : 4. Then the angles are
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
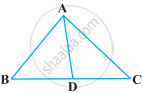
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.