Advertisements
Advertisements
प्रश्न
If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is
पर्याय
90°
180°
270°
360°
उत्तर
n the given ΔABC, all the three sides of the triangle are produced. We need to find the sum of the three exterior angles so produced.
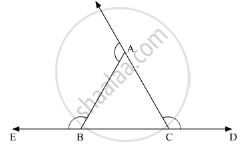
Now, according to the angle sum property of the triangle
∠A + ∠B + ∠C = 180° .......(1)
Further, using the property, “an exterior angle of the triangle is equal to the sum of two opposite interior angles”, we get,
ext.∠C = ∠A + ∠B ......(2)
Similarly,
ext.∠A = ∠C + ∠B .......(3)
Also,
ext.∠B = ∠C+ ∠A .......(4)
Adding (2) (3) and (4)
We get,
ext.∠A + ext.∠B+ ext.∠C = ∠C+∠B +∠C +∠A + ∠B + ∠A
= 2(∠A= ∠B+ ∠C )
= 2 (180°)
= 360°
Thus, ext. ∠A + ext. ∠B ext.∠C = 360°
APPEARS IN
संबंधित प्रश्न
Can a triangle have two obtuse angles? Justify your answer in case.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
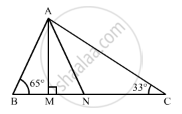
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
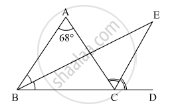
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
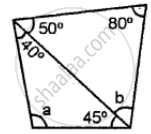
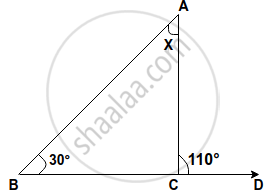
In the following, find the marked unknown angle:
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
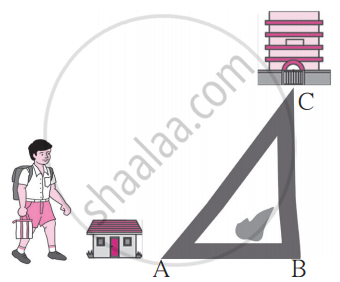
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
