Advertisements
Advertisements
प्रश्न
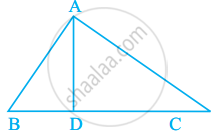
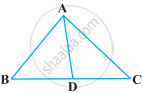
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
उत्तर
Given: ABC is a triangle such that AD is the bisector of ∠BAC.
To prove: AB > BD.
Proof: Since, AD is the bisector of ∠BAC.
But ∠BAD = CAD ...(i)
∴ ∠ADB > ∠CAD ...[Exterior angle of a triangle is greater than each of the opposite interior angle]
∴ ∠ADB > ∠BAD ...[From equation (i)]
AB > BD ...[Side opposite to greater angle is longer]
Hence proved.
APPEARS IN
संबंधित प्रश्न
Fill in the blank to make the following statement true:
An exterior angle of a triangle is always ......... than either of the interior opposite angles.
If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
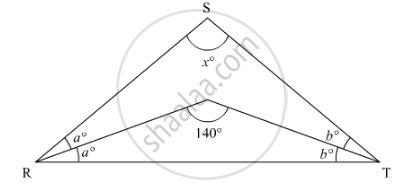
In ΔRST (See figure), what is the value of x?
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
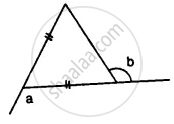
In the given figure, express a in terms of b.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
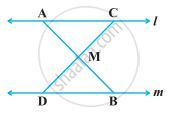
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
The number of angles in figure is ______.
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.