Advertisements
Advertisements
Question
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
Solution
Given: In ΔABC, D is the mid-point of AC i.e., AD = CD such that BD = `1/2` AC.
To show: ∠ABC = 90°
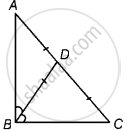
Proof: We have BD = `1/2` AC ...(i)
Since, D is the mid-point of AC.
∴ AD = CD = `1/2` AC ...(ii)
From equations (i) and (ii),
AD = CD = BD
In ΔDAB, AD = BD ...[Proved above]
∴ ∠ABD = ∠BAD ...(iii) [Angles opposite to equal sides are equal]
In ΔDBC, BD = CD ...[Proved above]
∴ ∠BCD = ∠CBD ...(iv) [Angles opposite to equal sides are equal]
In ΔABC, ∠ABC + ∠BAC + ∠ACB = 180° ...[By angle sum property of a triangle]
⇒ ∠ABC + ∠BAD + ∠DCB = 180°
⇒ ∠ABC + ∠ABD + ∠CBD = 180° ...[From equations (iii) and (iv)]
⇒ ∠ABC + ∠ABC = 180°
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
APPEARS IN
RELATED QUESTIONS
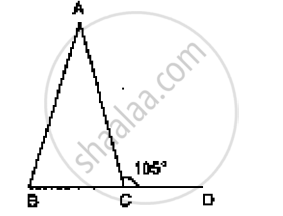
In Figure AB = AC and ∠ACD =105°, find ∠BAC.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Which of the following statements are true (T) and which are false (F) :
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
Which of the following statements are true (T) and which are false (F)?
Sum of any two sides of a triangle is greater than the third side.
Fill in the blank to make the following statement true.
The sum of three altitudes of a triangle is ..... than its perimeter.
Fill in the blank to make the following statement true.
If two angles of a triangle are unequal, then the smaller angle has the........ side opposite to it.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
