Advertisements
Advertisements
Question
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Solution
Yes, In ΔABC, M is a point of side BC such that AM is the bisector of ∠BAC.
In ΔABM, AB + BM > AM ...(i) [Sum of two sides of a triangle is greater than the third side]
In ΔACM, AC + CM > AM ...(ii) [Sum of two sides of a triangle is greater than the third side]
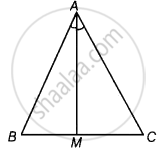
On adding equations (i) and (ii), we get
(AB + BM + AC + CM) > 2AM
⇒ (AB + BM + MC + AC) > 2AM
⇒ AB + BC + AC > 2AM ...[∵ BC = BM + MC]
∴ Perimeter of ΔABC > 2AM
APPEARS IN
RELATED QUESTIONS
Find the measure of each exterior angle of an equilateral triangle.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ΔABC is equilateral.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that LN = MN.
Fill in the blank to make the following statement true.
Difference of any two sides of a triangle is........ than the third side.
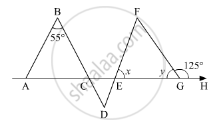
In the given figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
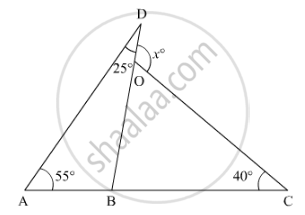
In the given figure, the value of x is ______.
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
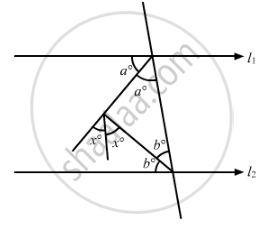
In the given figure, if l1 || l2, the value of x is
D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.
