Advertisements
Advertisements
प्रश्न
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

उत्तर
In △ABD and △CBD
seg AB = seg CB ...(Given)
seg AD = seg CD ...(Given)
seg BD = seg BD ...(Common side)
△ABD ≅ △CBD ...(SSS test)
APPEARS IN
संबंधित प्रश्न
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
If ΔPQR≅ ΔEFD, then ∠E =
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
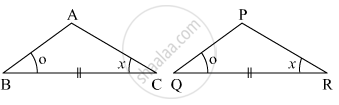
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
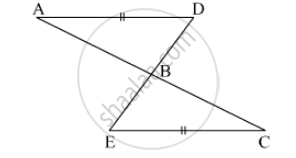
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.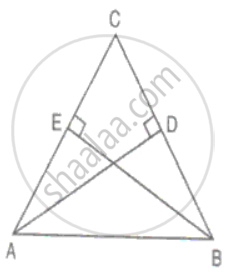
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
If AB = QR, BC = PR and CA = PQ, then ______.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
