Advertisements
Advertisements
Question
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes ?
Solution
The sides of a triangle are a = 35 cm, b = 54 cm and c = 61 cm
Now, perimeter a + b + c = 25
`⇒S= 1/2(35+54+61)`
⇒s= 75cm
By using heron’s formula
∴Area of triangle =`sqrt(s(s-a)(s-a)(s-c))`
`=sqrt(75(75-35)(75-54)(75-61))`
`sqrt(75(40)(21)(14))=93914cm^2`
∴ The altitude will be a smallest when the side corresponding to it is longest Here, longest side is 61 cm
∴ area altitude will be a smallest when the side corresponding to is longest here' longest side is 61 cm
∴area of Δ le = `1/2xxbxxh= 1/2xx base xx height `
`∴1/2xxhxx61= 939.14`
`⇒= (939.14xx2)/61= 30.79 cm`
๐ป๐๐๐๐ ๐กโ๐ ๐๐๐๐๐กโ ๐๐ ๐กโ๐ ๐ ๐๐๐๐๐๐ ๐ก ๐๐๐ก๐๐ก๐ข๐๐ ๐๐ 30.79 ๐๐
APPEARS IN
RELATED QUESTIONS
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Determine whether the sets of points are collinear?
`(-1/2, 3), (-5, 6) and (-8, 8)`
Find the area of triangle AGF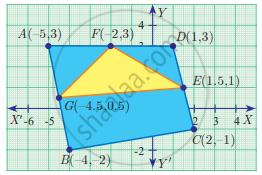
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
