Advertisements
Advertisements
Question
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Advertisements
Solution
Let the sides of a triangle are 3x, 4x and 5x.
Now, a = 3x, b = 4x and c = 5x
The perimeter 2s = 144
⇒ 3x + 4x + 5x = 144 [∵ a + b + c = 2s]
⇒ 12x = 144
⇒ x = 12
∴ sides of triangle are a = 3(x) = 36cm
b = 4(x) = 48 cm
c = 5(x) = 60 cm
Now semi perimeter s`1/2(a+b+c)=1/2(144)=72cm`
By heron’s formulas ∴ Area of Δle = `sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(72(72-36)(72-48)(72-60)`
`=864cm^2`
Let l be the altitude corresponding to longest side,∴`1/2xx60xxl=864`
`⇒l=(864xx2)/60`
`⇒l=28.8cm`
Hence the altitude one corresponding long side = 28.8 cm
APPEARS IN
RELATED QUESTIONS
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
A triangular shaped glass with vertices at A(– 5, – 4), B(1, 6) and C(7, – 4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
The perimeter of an equilateral triangle is 30 cm. The area is
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is ______.
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
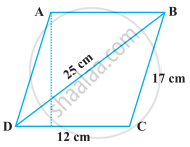
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.
