Advertisements
Advertisements
Question
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution
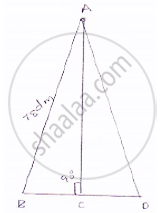
ABC be the triangle, Here a = 78 dm = AB,
BC = b = 50 dm
Now, perimeter = 240 dm
⇒ AB + BC + CA = 240 dm
⇒ AC = 240 – BC – AB
⇒ AC = 112 dm
Now, 2s = AB + BC + CA
⇒ 2s = 240
⇒ s = 120 dm
∴ Area of ΔABC =`sqrt(s(s-a)(s-b)(s-b))` by heron's formula
=`sqrt(120(120-78)(120-50)(120-112))`
`=sqrt(120xx42xx70xx8)`
1680 `dm^2`
๐ฟ๐๐ก ๐ด๐ท ๐๐ ๐๐๐๐๐๐๐๐๐๐ข๐๐๐๐ ๐๐ ๐ต๐ถ
Area of ΔABC = `1/2xx ABxxBC `(area of triangle=`(1/2xxbxxh)`
`=1/2xx ADxxBC=1680 `
`⇒AD=(2xx1680)/50=67.2dm`
APPEARS IN
RELATED QUESTIONS
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Find the area of the triangle formed by the points
(1, – 1), (– 4, 6) and (– 3, – 5)
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
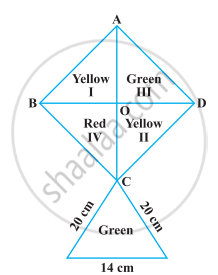
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.
