Advertisements
Advertisements
Question
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
Solution
Given: The perimeter of a triangle is 50 cm.
Now, semi-perimeter(s) of the triangle is
= `"Perimeter of triangle"/2`
= `50/2`
= 25
Suppose that the smaller side of the triangle be a = x cm.
So, the second side will be b = (x + 4) cm and 3rd side will be c = (2x – 6) cm.
Now, perimeter of triangle = a + b + c = x + (x + 4) + (2x – 6)
50 cm = (4x – 2) cm
50 = 4x – 2
4x = 50 + 2
4x = 52
x = `52/4`
x = 13
Since, the three side of the triangle are:
a = x = 13,
b = x + 4 = 13 + 4 = 17
c = 2x – 6 = 2 × 13 – 6 = 26 – 6 = 20.
So, area of the triangle = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(25 xx (25 - 13) xx (25 - 17) xx (25 - 20))`
= `sqrt(25 xx 12 xx 8 xx 5)`
= `sqrt(5 xx 5 xx 4 xx 3 xx 4 xx 2 xx 5)`
= `5 xx 4 xx 20sqrt(30) cm^2`
= `20sqrt(30) cm^2`
Therefore, the area of a triangle is `20sqrt(30) cm^2`.
APPEARS IN
RELATED QUESTIONS
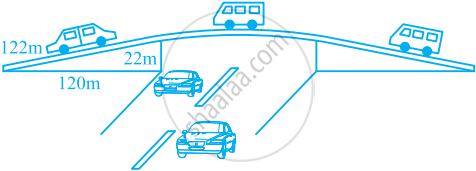
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Find the area of the triangle formed by the points
(1, – 1), (– 4, 6) and (– 3, – 5)
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
The sides of the triangular ground are 22 m, 120 m and 122 m. Find the area and cost of levelling the ground at the rate of ₹ 20 per m2
A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
