Advertisements
Advertisements
Question
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Advertisements
Solution
Let us join BD.
In ΔBCD, applying Pythagoras theorem,
BD2 = BC2 + CD2
= (12)2 + (5)2
= 144 + 25
BD2 = 169
BD = 13 m
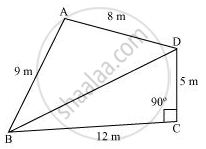
Area of ΔBCD
`= 1/2xxBCxxCD = (1/2xx12xx5)m^2=30m^2`
For ΔABD,
`s="Perimeter"/2=(9+8+12)/2=15m`
By Heron's formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of "triangleABD=[sqrt(15(15-9)(15-8)(15-13))]m^2`
`=(sqrt(15xx6xx7xx2))m^2`
`=6sqrt35 m^2`
= (6 x 5.916) m2
= 35.496 m2
Area of the park = Area of ΔABD + Area of ΔBCD
= 35.496 + 30 m2
= 65.496 m2
= 65.5 m2 (approximately)
RELATED QUESTIONS
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
Find the area of an equilateral triangle having each side 4 cm.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
If each side of a triangle is doubled, the find percentage increase in its area.
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
If the area of an equilateral triangle is `16sqrt(3)` cm2, then the perimeter of the triangle is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
