Advertisements
Advertisements
Question
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
Solution

Perimeter of the rhombus = 160 m
4 × side = 160
Side of a rhombus = `160/4`
= 40 m
In ΔABC, a = 40 m, b = 40 m, c = 48 m
s = `("a" + "b" + "c")/2`
= `(40 + 40 + 48)/2 "cm"`
= `128/2`
= 64 m
s – a = 64 – 40 = 24 m
s – b = 64 – 40 = 24 m
s – c = 64 – 48 = 16m
Area of the ΔABC = `sqrt(64 xx 24 xx 24 xx 16)`
= 8 × 24 × 4
= 768 sq.m
Since ABCD is a rhombus Area of two triangles are equal.
Area of the rhombus ABCD = (768 + 768) sq.m
= 1536 sq.m
∴ Area of the land = 1536 sq.m
APPEARS IN
RELATED QUESTIONS
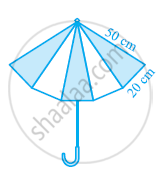
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of an equilateral triangle having each side x cm.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
