Advertisements
Advertisements
Question
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is
Options
- \[30\sqrt{7} cm\]
- \[\frac{15\sqrt{7}}{2}cm\]
- \[\frac{15\sqrt{7}}{4}cm\]
30 cm
Solution
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
`A= sqrt(s(s-a)(s-b)(s-c))`, where
`s = (a+b+c)/2`
We need to find the altitude corresponding to the longest side
Therefore the area of a triangle having sides 11 cm, 15 cm and 16 cm is given by
a = 11 m ; b = 15 cm ; c = 16 cm
`s = (a+b+c)/2`
`s =(11+15+16)/2`
`s = 42/2`
s = 21 cm
`A = sqrt(21(21-11)(21-15)(21-6))`
`A = sqrt(21(10)(6)(5)`
`A = sqrt(6300)`
`A = 30 sqrt(7) cm^2`
The area of a triangle having base AC and height p is given by
`"Area (A) " = 1/2 ("Base" xx "Height")`
`"Area(A)" = 1/2 (AC xx p)`
We have to find the height p corresponding to the longest side of the triangle.Here longest side is 16 cm, that is AC=16 cm
`30 sqrt(7) = 1/2 (16 xx p)`
`30 sqrt(7) xx 2 = (16 xx p)`
` p = (30sqrt(7) xx 2) /16`
`p = (15 sqrt(7) )/4 cm `
APPEARS IN
RELATED QUESTIONS
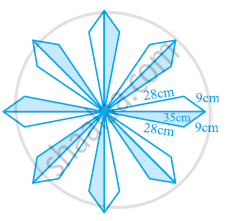
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
If every side of a triangle is doubled, then increase in the area of the triangle is
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
The perimeter of an equilateral triangle is 60 m. The area is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
