Advertisements
Advertisements
Question
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
Solution
Given that,
Perimeter of rhombus = 80m
Perimeter of rhombus = 4 × side
⇒ 4a = 80
⇒ a = 20m
Let AC = 24 m
∴ OA =`1/2AC=1/2xx24=12m`
In ΔAOB
`OB^2=AB^2-OA^2`
`⇒OB=sqrt(20^2-12^2)`
`sqrt(400-144)`
`sqrt(256)=16m`
Also BO = OD
[Diagonal of rhombus bisect each other at 90°]
∴ BD = 20B = 2 ×16 = 32 m
∴Area of rhombus = `1/2`×32×24=`384𝑚^2`
[∵Area of rhombus = 12×𝐵𝐷×𝐴𝐶]
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
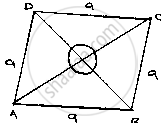
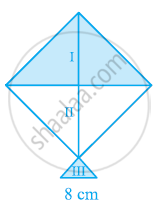
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
The sides of a triangle are 50 cm, 78 cm and 112 cm. The smallest altitude is
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
