Advertisements
Advertisements
प्रश्न
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
उत्तर
The co-ordinates of the midpoint `(x_m,y_m)` between two points `(x_1,y_1)` and (x_2,) is given by,
`(x_m,y_m) = (((x_1+x_2)/2)"," ((y_1+y_2)/2))`
`Let the three vertices of the triangle be `A(x_A,y_A), B(x_B, y_B)` and `C(x_C, y_C)`.
The three midpoints are given. Let `these points be `M_(AB)` (3,4), `M_(BC)` (4, 6)`and `M_(CA) (5, 7)`.
Let us now equate these points using the earlier mentioned formula,
`(3,4) = (((x_A + x_B)/2)"," ((y_A + y_B)/2))`
Equating the individual components we get,
`x_A + x_B = 6`
`y_A + y_B = 8`
Using the midpoint of another side we have,
`(4,6) = (((x_B + x_C)/2)","((y_B + y_C)/2))`
Equating the individual components we get,
`x_B + x_C = 8`
`y_B + y_C = 12`
Using the midpoint of the last side we have,
`(5,7) = (((x_A + x_C)/2)","((y_A + y_C)/2))`
Equating the individual components we get,
`x_A + x_C = 10`
`y_A + y_C = 14`
Adding up all the three equations which have variable ‘x’ alone we have,
`x_A + x_B + x_B + x_C + x_A + x_C = 6 + 8 + 10`
`2(x_A + x_B + x_C) = 24`
`x_A + x_B + x_C = 12`
Substituting `x_B + x_C = 4` in the above equation we have,
`x_A + x_B + x_C = 12`
`x_A + 8 = 12`
`x_A = 4`
Therefore,
`x_A + x_C = 10`
`x_C = 10 - 4`
`x_C = 6`
And
`x_A + x_B = 6`
`x_B = 6 - 4`
`x_B = 2`
Adding up all the three equations which have variable ‘y’ alone we have,
`y_A + y_B + y_B + y_C + y_A + y_C = 8 + 12 + 14`
`2(y_A + y_B + y_C) = 34`
`y_A + y_B + y_C = 17`
Substituting `y_B + y_C = 12` in the above equation we have
`y_A + y_B + y_C = 17`
`y_A + 12 = 17`
`y_A = 5`
Therefore
`y_A + y_C = 14`
`y_C = 14 - 5`
`y_C = 9
And
`y_A + y_B = 8`
`y_C = 14 - 5`
`y_C = 9`
And
`y_A + y_B = 8`
`y_B = 8 - 5`
`y_B = 3`
Therefore the co-ordinates of the three vertices of the triangle are A(4,5), B(2,3), C(6,9)
APPEARS IN
संबंधित प्रश्न
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
A(6,1) , B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
Find the area of the following triangle:

The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
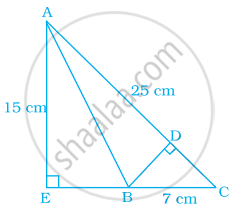
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.