Advertisements
Advertisements
प्रश्न
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

उत्तर
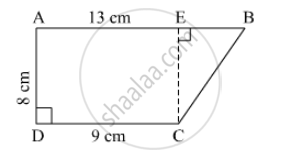
Draw perpendicular from C to line AB. Name the point E.
CE = AD = 8 cm
EB = AB − AE = AB − CD = 13 − 9 = 4cm
∴ Area of of a trapezium = `1/2 xx "sum of lengths of parallel sides" xx h`
A (☐ABCD) = `1/2 xx [l(AB) + l(DC)] xx l(AD)`
= `1/2 xx (13 + 9) xx 8`
= `1/2 xx 22 xx 8`
= 11 x 8
= 88 sq. cm
∴ The area of ☐ABCD is 88 sq. cm.
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
Find the area of the following triangle:

If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then ____________.
