Advertisements
Advertisements
Question
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq cm, find its perimeter.
Solution
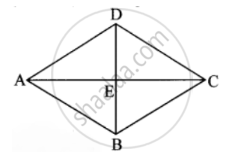
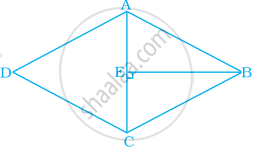
Let ABCD be the rhombus.
Diagonals AC and BD intersect at point E.
l(AC) = 30 cm …(i)
and Area of a rhombus = 240 sq. cm …(ii)
Area of a rhombus = `1/2` (product of diagnols)
⇒ 240 = `1/2` × (30 × DB)
⇒ DB = `(240 xx 2)/30` = 16 …(iii)
Diagonals of a rhombus bisect each other.
∴ `l(AE) = 1/2 l(AC)`
= `1/2 xx 30`
= 15 cm …(iv)
∴ `l(DE) = 1/2 l(DB)`
= `1/2 xx 16`
= 8 cm …(v)
In ΔADE,
∠AED = 90° …[Diagonals of a rhombus are perpendicular to each other]
AE2 + DE2 = AD2 …[Pythagoras theorem]
⇒ 152 + 82 = AD2 ...[From (iv) and (v)]
⇒ AD2 = 225 + 64 = 289
⇒ AD = `sqrt289` …[Taking square root of both sides]
= 17 cm
Thus, the side of the rhombus = 17 cm
Perimeter of rhombus = 4 × side
= `4 xx 17`
= 68 cm
∴ The perimeter of the rhombus is 68 cm.
RELATED QUESTIONS
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
The diagonals of a rhombus are 18 cm and 24 cm. Find:
(i) its area ;
(ii) length of its sides.
(iii) its perimeter
Find the area of rhombus PQRS shown in the following figure.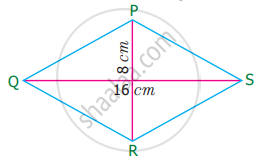
Find the area of rhombus PQRS shown in the following figure.
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 19 cm | 16 cm |
A sweet is in the shape of rhombus whose diagonals are given as 4 cm and 5 cm. The surface of the sweet should be covered by an aluminum foil. Find the cost of aluminum foil used for 400 such sweets at the rate of ₹ 7 per 100 sq.cm
The area of the rhombus with side 4 cm and height 3 cm is
The figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is ______.

What is the area of the rhombus ABCD below if AC = 6 cm and BE = 4 cm?
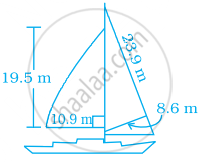
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.