Advertisements
Advertisements
Question
The diagonals of a rhombus are 18 cm and 24 cm. Find:
(i) its area ;
(ii) length of its sides.
(iii) its perimeter
Advertisements
Solution
The diagonal of the rhombus is 18 cm and 24 cm.
area of rhombus = `1/2` x Product of diagonals
= `1/2` x 18 x 24
= 216 cm2
(ii)
Diagonals of a rhombus bisect each other at right angles.
∴ OA = `1/2 xx 24 = 12` cm
OB = `1/2 xx 18 = 9` cm
In right ∠d Δ AOB
AB = `sqrt("OA"^2 + "OB"^2)`
= `sqrt((12)^2 + (9)^2)`
= `sqrt(144 + 81)`
= `sqrt(225) = 15` cm
∴ Side of rhombus = 15 cm
(iii)
Perimeter of rhombus = `4 xx "side"`
= `4 xx 15 = 60` cm
(i) 216 cm2 (ii) 15 cm (iii) 60 cm.
APPEARS IN
RELATED QUESTIONS
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq cm, find its perimeter.
The length of the diagonals of a rhombus is in ratio 4 : 3. If its area is 384 cm2, find its side.
Find the area of rhombus PQRS shown in the following figure.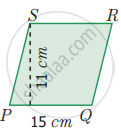
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 19 cm | 16 cm |
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 26 m | 468 sq.m |
The figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is ______.
Area of a quadrilateral ABCD is 20 cm2 and perpendiculars on BD from opposite vertices are 1 cm and 1.5 cm. The length of BD is ______.
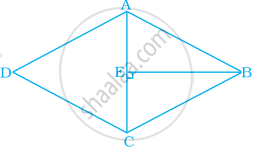
Area of a rhombus = `1/2` product of ______.
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of sail of the sailboats to the nearest tenth.
