Advertisements
Advertisements
Question
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
Solution

Perimeter of the rhombus = 100 cm
⇒ `4 xx` side = 100
⇒ side = `100/4` = 25 cm
Thus, each side of the rhombus = 25 cm.
Diagonals of a rhombus are perpandicular bisector of each other.
So, AO = OC = `48/2` = 24 cm
In Δ AOB,
We apply Pythagoras theorem,
AO² + OB² = AB²
⇒ 24² + OB² = 25²
⇒ OB² = 625 - 576 = 49
⇒ OB = 7 cm
So, DB = `2 xx "OB" = 2 xx 7` = 14 cm
Area of rhombus = `1/2 xx` (product of diagonal)
= `1/2 xx 14 xx 48`
= 336 cm²
RELATED QUESTIONS
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
Each side of a rhombus is 18 cm. If the distance between two parallel sides is 12 cm, find its area.
The diagonals of a rhombus are 18 cm and 24 cm. Find:
(i) its area ;
(ii) length of its sides.
(iii) its perimeter
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm; find:
- It's other diagonal
- area
Find the area of rhombus PQRS shown in the following figure.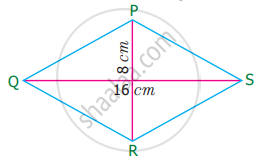
Find the area of rhombus PQRS shown in the following figure.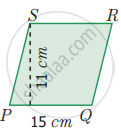
The area of a rhombus is 100 sq.cm and length of one of its diagonals is 8 cm. Find the length of the other diagonal
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
Area of a rhombus = `1/2` product of ______.
