Advertisements
Advertisements
Question
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
Solution
A( 3,8) , B(-4,2) and C( 5, -1) are the vertices of ΔABC . Then,
`(x_1 =3, y_1=8),(x_2=-4,y_2=2) and (x_3=5,y_3=-1)`
Area of triangle ABC
`=1/2 {x_1(y_2-y_3) + x_2(y_3-y_1) +x_3(y_1-y_2)}`
`=1/2 {3(2-(-1))+(-4)(-1-8)+5(8-2)}`
`=1/2 {3(2+1)-4(-9)+5(6)}`
`=1/2 {9+36+30}`
`=1/2(75)`
=37.5 sq . units
APPEARS IN
RELATED QUESTIONS
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
Find the area of the following triangle:
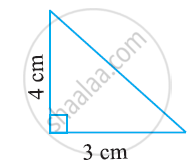
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

What is the area of a triangle with base 4.8 cm and height 3.6 cm?
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
