Question

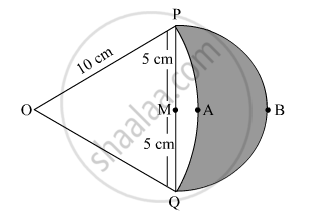
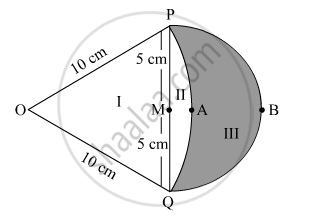
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.

Answer 1

Given: OP = OQ = 10 cm

It is known that tangents drawn from an external point to a circle are equal in length.

So,
OP = OQ = 10 cm

Therefore, ∆ABC is an equilateral triangle.

⇒∠POQ=60°

Now

Area of part II = Area of the sector − Area of the equilateral triangle POQ

`=(/_POQ)/360^@xxpir^2-sqrt3/4xx(10)^2`

`=60^@/360^@xxpi(10^2)-sqrt3/4xx(10)^2`

`=100(pi/6-sqrt3/4) `

Area of the semicircle on diameter PQ = Area of part II + Area of part III

`1/2xxpi(5)^2=25/2pi`

 ∴ Area of the shaded region (part III)

`=25/2pi-100(pi/6-sqrt3/4)`

`=25/2pi-100/6pi+25sqrt3`

`=25sqrt3-25/6pi`

`=25(sqrt3-pi/6)`

Hence proved.