Advertisements
Advertisements
प्रश्न
Sum of the areas of two squares is 157 m2. If the sum of their perimeters is 68 m, find the sides of the two squares.
उत्तर
Let the side of one square be x
And a side of other square be y
Sum of an area of two square is 157
Equation becomes
`x^2 + y^2 = 157` ....(1) (∵ area of square is side2)
Now, sum of their perimeters is 68
Equation becomes
`4x + 4y = 68` (∵ perimeter of square is 4 × side)
solving the two-equation by substitution method
`4x + 4y = 68`
`x + y = 17`
⇒ x = 17 - y ....(2)
Substitute (2) in (1)
`(17 - y)^2 + y^2 = 157`
`289 + y^2 - 34y + y^2 = 157`
`2y^2 - 34y + 132 = 0`
`y^2 - 17y + 66 = 0`
Using y = `(-b ± sqrt(b^2 - 4ac))/(2a)`
Plugging the values in the formula we get
`y = (17 ± sqrt(289 - 4(66)))/2`
`y = (17 ± sqrt(25))/2`
`y = (17 ± 5)/2`
`y = 12/2,22/2`
y = 6,11
when y = 6 then x = 11
And when y = 11 then x = 6
Therefore, the sides of square are 6 m and 11 m.
APPEARS IN
संबंधित प्रश्न
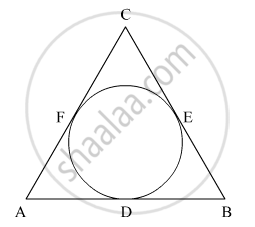
In Fig. 2, a circle is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA and 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.
The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in one minute. (Use π = 22/7)
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
28 mm
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
How many times a wheel of radius 28 cm must rotate to go 352 m? (Take `pi = 22/7`)
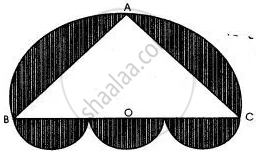
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
Find the area and perimeter of the circle with the following :
Radius= 2.8 cm
Find the area and perimeter of the circle with the following:
Diameter= 35 cm
Find the area and perimeter of the circles with following: Radius = 2.8cm
Formula used to find the circumference of a circle is
