Advertisements
Advertisements
Question
Sum of the areas of two squares is 157 m2. If the sum of their perimeters is 68 m, find the sides of the two squares.
Solution
Let the side of one square be x
And a side of other square be y
Sum of an area of two square is 157
Equation becomes
`x^2 + y^2 = 157` ....(1) (∵ area of square is side2)
Now, sum of their perimeters is 68
Equation becomes
`4x + 4y = 68` (∵ perimeter of square is 4 × side)
solving the two-equation by substitution method
`4x + 4y = 68`
`x + y = 17`
⇒ x = 17 - y ....(2)
Substitute (2) in (1)
`(17 - y)^2 + y^2 = 157`
`289 + y^2 - 34y + y^2 = 157`
`2y^2 - 34y + 132 = 0`
`y^2 - 17y + 66 = 0`
Using y = `(-b ± sqrt(b^2 - 4ac))/(2a)`
Plugging the values in the formula we get
`y = (17 ± sqrt(289 - 4(66)))/2`
`y = (17 ± sqrt(25))/2`
`y = (17 ± 5)/2`
`y = 12/2,22/2`
y = 6,11
when y = 6 then x = 11
And when y = 11 then x = 6
Therefore, the sides of square are 6 m and 11 m.
APPEARS IN
RELATED QUESTIONS
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
The sum of the radii of two circles is 140 cm and the difference of their circumferences in 88 cm. Find the diameters of the circles.
Choose the correct alternative answer for the following question.
A circus tent is cylindrical to a height of 5 m and conical above it. If its diameter is 42 m and slant height of the cone is 53 m, calculate the total area of the canvas required.
The circumference of a circle is eigth time the circumference of the circle with a radius of 12 cm. Find its diameter.
Find the area of a circular field that has a circumference of 396m.
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 56 m
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where `pi = 22/7` then length of an arc is ____________.
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the below figure:
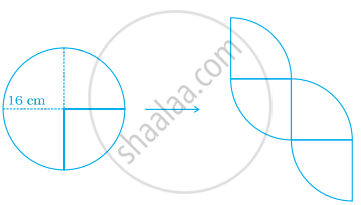
Does the perimeter change? If it does change, by how much does it increase or decrease?
Find the total cost of wooden fencing around a circular garden of diameter 28 m, if 1 m of fencing costs ₹ 300.
