Advertisements
Advertisements
प्रश्न
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
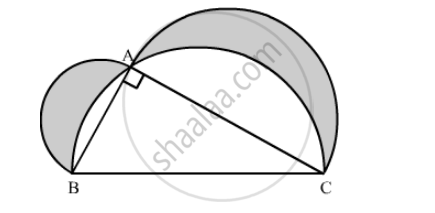
उत्तर
We have given three semi-circles and one right angled triangle.
`"∴ Area ofshaded region=Area of semi-circle with AB as a diameter"`
`"+ Area of semi-circle with AC as a diameter"`
`"+ Area of right angled ABC"`
` "-Area of semi-circle with BC as a diameter"`
Let us calculate the area of the semi-circle with AB as a diameter.
`∴"Area of semi-circle with AB as a diameter"=(pir^2)/2`
`∴ "Area of semi-circle with AB as a diameter"=pi/2(21/2)^2`
` "Area of semi-circle with AB as a diameter"=pi/2(21/2)^2`
Now we will find the area of the semi-circle with AC as a diameter.
`"Area of semi-circle with AC as a diameter"=pir^2/2`
`"Area of semi-circle with AC as a diameter"pi(28/2)^2/2`
`"Area of semi-circle with AC as a diameter"pi/2(28/2)^2`
Now we will find the length of BC.
In right angled triangle ABC, we will use Pythagoras theorem,
`BC^2=AB^2+AC^2`
`∴ BC^2=21^2+28^2`
`∴BC^2=441+784`
`∴BC^2=1225`
`∴ BC=35`
Now we will calculate the area of the right angled triangle ABC.
`A(ΔABC)=1/2xxABxxAC`
`∴ A(ΔABC)=1/2xx21xx28`
`∴A(ΔABC)=21xx14`
`∴ A(ΔABC)=294`
Now we will find the area of the semi-circle with BC as a diameter.
`"Area of semi-circle with BC as a diameter"=`(pi r^2)/2`
`∴" Area of semi-circle with AB as a diameter"=pi(35/2)^2/2`
`∴ " Area of semi-circle with AB as a diameter"=pi/2(35/2)^2`
Now we will substitute all these values in equation (1).
`∴ "Area of the shaded region"=pi/2(21/2)^2+pi/2(28/2)^2+294-pi/2(35/2)^2`
`∴ "Area of the shaded region"=pi/8(21^2+28^2-35^2)+294`
`∴ "Area of the shaded region"=pi/8(441+784-1225)+294`
`∴"Area of the shaded region"pi/8(1225-1225)+294`
`∴"Area of the shaded region"=294`
Therefore, area of shaded region is `294 cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of the following circle, given that radius = 14 mm (take `pi = 22/7`).
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
Write the area of the sector of a circle whose radius is r and length of the arc is l.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
If the circumference of a circle increases from 4π to 8π, then its area is
If the radius of a circle is diminished by 10%, then its area is diminished by
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
