Advertisements
Advertisements
प्रश्न
Write the area of the sector of a circle whose radius is r and length of the arc is l.
उत्तर
We know that area of the sector of the circle of radius `r= θ/360xxpir^2`
But we have given that length of the arc =l
So, `l=θ/360xx2pir`.............(1)
`"Area of the sector"=θ/360xxpir`
Now we will adjust 2 in the following way,
`"Area of the sector"=θ/360xx(2pir^2)/2`
`"Area of the sector"=θ/360xx2pirxxr/2`
From equation (1) we will substitute` θ/360xx2pir=l`
Area of the sector =`lxxr/2`
Area of the sector=`1/2lr`
Therefore, area of the sector=`1/2 lr`
APPEARS IN
संबंधित प्रश्न
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
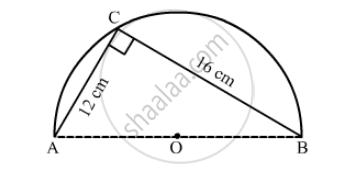
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
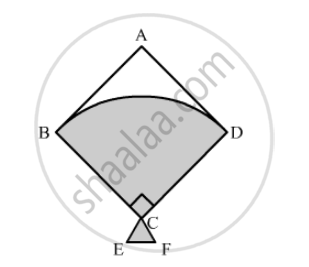
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
The area of a circular path of uniform width h surrounding a circular region of radius r is
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
A 7m wide road surrounds a circular garden whose area is 5544m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per m2.
