Advertisements
Advertisements
Question
Write the area of the sector of a circle whose radius is r and length of the arc is l.
Solution
We know that area of the sector of the circle of radius `r= θ/360xxpir^2`
But we have given that length of the arc =l
So, `l=θ/360xx2pir`.............(1)
`"Area of the sector"=θ/360xxpir`
Now we will adjust 2 in the following way,
`"Area of the sector"=θ/360xx(2pir^2)/2`
`"Area of the sector"=θ/360xx2pirxxr/2`
From equation (1) we will substitute` θ/360xx2pir=l`
Area of the sector =`lxxr/2`
Area of the sector=`1/2lr`
Therefore, area of the sector=`1/2 lr`
APPEARS IN
RELATED QUESTIONS
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
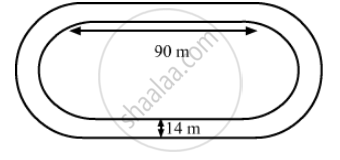
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
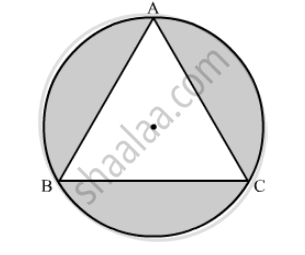
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
The area of a circle is 98.56 cm2. Find its circumference.
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
