Advertisements
Advertisements
Question
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

Solution
We have given two semi-circles and one circle.
Area of the shaded region = area of semicircle with diameter AB − area of two semicircles with diameters AM and MB - area of circle ……..(1)
Let us calculate the area of the semi-circle with AB as a diameter.
`"Area of semi-circle with AB as a diameter "= pir^2/2`
`∴ "Area of semi-circle with AB as a diameter "=(pi(36/2)^2)/2`
`"∴Area of semi-circle with AB as a diameter"=(pixx18^2)/2`
Now we will find the area of the semi-circle with AM as a diameter.
`"∴Area of semi-circle with AM as a diameter"=(pi r^2)/2`
`"∴Area of semi-circle with AM as a diameter"=pi(18/2)^2`
`"∴Area of semi-circle with AM as a diameter"=(pixx9^2)/2`
with diameter with AM as a diameter.
Now we will find the area of the circle with centre C.
Area of circle=`pir^2`
We know that radius of the circle is one sixth of AB
Area of circle=`pixx6^2`
Now we will substitute all these values in equation (1).
`∴"Area of shaded region"=(pixx18^2)/2-(pixx9^2)/2-(pixx9^2)/2-36pi`
`∴"Area of shaded region"=pixx18^2/2-pixx9^2-36pi`
`"∴Area of shaded region"=(pixx18^2)/2-81 pi-36pi`
`"∴ Area of shaded region"=(pixx18^2)/22-117pi`
`"∴Area of shaded region"=(162-117)pi`
`∴"Area of shaded region"=45pi`
Therefore, area of shaded region is `45 pi cm^2`
APPEARS IN
RELATED QUESTIONS
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
The area of the incircle of an equilateral triangle of side 42 cm is
In the following figure, the area of the segment PAQ is

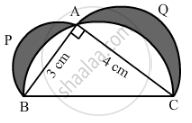
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
