Advertisements
Advertisements
प्रश्न
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
उत्तर १
Let the diameter of the three circles be 3d, 5d, and 6d respectively.
Now
π x 3d + π x 5d + π x 6d = 308
14πd = 308
d = 7
radius of the smallest circle = `21/2` = 10.5
Area = π x (10 .5)2
= 346.5
radius of the largest circle = `42/2` = 21
Area = π x ( 21 )2
= 1386
difference = 1386 - 346.5
= 1039.5 cm2
उत्तर २
Let the diameter of the first circle, d1 = 3x cm
Then diameter of the second circle, d2 = 5x cm
Diameter of the third circle, d3 = 6x cm
Now, sum of circumference of 3 circles = 308 cm
⇒ πd1+ πd2 + πd3 = 308
⇒ π[d1 + d2 + d3] = 308
⇒ `22/7`[3x + 5x + 6x ] = 308
⇒ `22/7` × 14x = 308
⇒ 44x = 308
⇒ x = 7
Now, diameter of smallest circle, d1 = 3x = 3 × 7 = 21 cm radius of smallest circle, r1 = `d_1/2 = (21/2)` cm
area of smallest circle = πr12 = `22/7 xx (21/2)^2` = 346.5cm2
Diameter of the largest circle, d2 = 6x = 6 × 7 = 42 cm
Now, radius of the largest circle, r2 = `(d_2/2)` = 21 cm
area of largest circle = πr22 = `22/7 xx (21)^2` = 1386 cm2
Difference between the areas = area of largest circle − area of smallest circle = 1386 − 346.5 = 1039.5 cm2
APPEARS IN
संबंधित प्रश्न
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
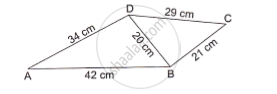
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

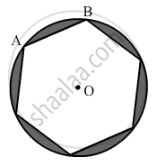
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
The area of a circle is 1386 sq.cm; find its circumference.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
