Advertisements
Advertisements
प्रश्न
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
उत्तर १
Let the diameter of the three circles be 3d, 5d, and 6d respectively.
Now
π x 3d + π x 5d + π x 6d = 308
14πd = 308
d = 7
radius of the smallest circle = `21/2` = 10.5
Area = π x (10 .5)2
= 346.5
radius of the largest circle = `42/2` = 21
Area = π x ( 21 )2
= 1386
difference = 1386 - 346.5
= 1039.5 cm2
उत्तर २
Let the diameter of the first circle, d1 = 3x cm
Then diameter of the second circle, d2 = 5x cm
Diameter of the third circle, d3 = 6x cm
Now, sum of circumference of 3 circles = 308 cm
⇒ πd1+ πd2 + πd3 = 308
⇒ π[d1 + d2 + d3] = 308
⇒ `22/7`[3x + 5x + 6x ] = 308
⇒ `22/7` × 14x = 308
⇒ 44x = 308
⇒ x = 7
Now, diameter of smallest circle, d1 = 3x = 3 × 7 = 21 cm radius of smallest circle, r1 = `d_1/2 = (21/2)` cm
area of smallest circle = πr12 = `22/7 xx (21/2)^2` = 346.5cm2
Diameter of the largest circle, d2 = 6x = 6 × 7 = 42 cm
Now, radius of the largest circle, r2 = `(d_2/2)` = 21 cm
area of largest circle = πr22 = `22/7 xx (21)^2` = 1386 cm2
Difference between the areas = area of largest circle − area of smallest circle = 1386 − 346.5 = 1039.5 cm2
APPEARS IN
संबंधित प्रश्न
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
A rectangular park is 100 m by 50 m. It is surrounding by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre (use π = 3.14).
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
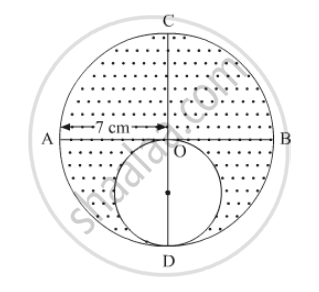
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
Area of the circle obtained in 196 m2 is ______.
If the radius of a semi-circular protractor is 7cm, then its perimeter is ______.
