Advertisements
Advertisements
प्रश्न
The area of a circular path of uniform width h surrounding a circular region of radius r is
पर्याय
\[\pi(2r + h)r\]
\[\pi(2r + h)r\]
\[\pi(2r + h)h\]
\[\pi(h + r)r\]
\[\pi(h + r)h\]
उत्तर

We have
`OA=r`
`AB=h`
Therefore, radius of the outer circle will be.`r+h`
Now we will find the area between the two circles.
∴Area of the circular path=`pi(r+h)^2-pir^2`
∴Area of the circular path=`pi(r^2+2rh+h^2)-pir^2`
∴Area of the circular path=`pi(r^2+2rh+h^2-r^2)`
Cancelling `r^2 "we get"`
∴Area of the circular path=`pi(2rh+h^2)`
∴Area of the circular path=`pi(2r+h)h`
Therefore,are of the circle is `pi(2r+h)h`
APPEARS IN
संबंधित प्रश्न
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
If diameter of a circle is increased by 40%, then its area increase by
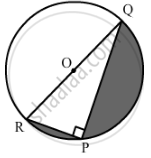
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
On increasing the diameter of a circle by 40%, its area will be increased by
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
Lalitha wants to buy a round carpet of radius is 63 cm for her hall. Find the area that will be covered by the carpet
Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
