Advertisements
Advertisements
प्रश्न
On increasing the diameter of a circle by 40%, its area will be increased by
पर्याय
40%
80%
96%
82%
उत्तर
96%
Let d be the original diameter.
Radius `="d"/2`
Thus, we have;
Original area `= π xx ("d"/2)`
`= (pi"a"^2)/4`
New diameter = 140% of d
`= (140/100xx"d")`
`= (7"d")/5`
Now,
New radius ` =(7"d")/5xx2`
`=(7"d")/10`
New area `= pixx((7"d")/10)^2`
`=(49π"a""^2)/10`
Increase in the area`=((49pi"a"^2)/10 - (pi"a"^2)/4)``
`=(24π"a"^2)/100`
`=(6pi"a"^2)/25 `
We have ;
Increase in the area`=((6pi"a"^2)/25xx4/(pi"a"^2)xx100)%`
= 96 %
APPEARS IN
संबंधित प्रश्न
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
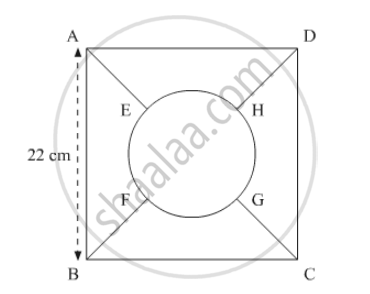
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
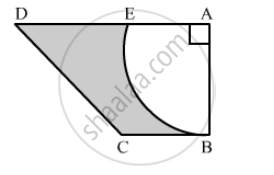
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
A square is inscribed in a circle of radius 6 cm. Find the area of the square. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
Find the area of a circle of radius 30 cm (use π = 3.14).
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
If the radius of a semi-circular protractor is 7cm, then its perimeter is ______.
