Advertisements
Advertisements
प्रश्न
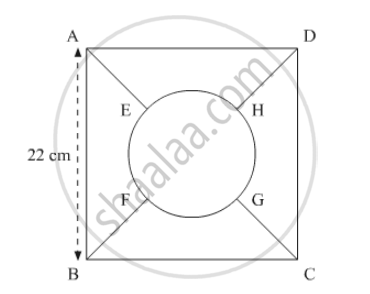
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
उत्तर
We have a square ABCD.

We have,
`AB=22 cm`
We have to find the perimeter of the triangle. We have a relation as,
Area of circular region=`1/5("Area of" ABCD)`
So,
`pir^2=1/5(22)^2`
`r=22/sqrt5pi`
`=5.56`
So perimeter of the circular region,
`=2pi r`
`=(22)22/7(22/sqrt(5pi))`
APPEARS IN
संबंधित प्रश्न
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
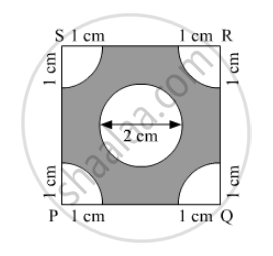
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
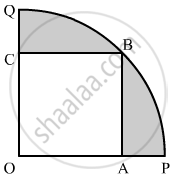
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
On decreasing the radius of a circle by 30%, its area is decreased by
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).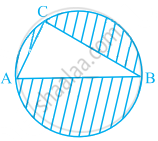
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
