Advertisements
Advertisements
Question
On increasing the diameter of a circle by 40%, its area will be increased by
Options
40%
80%
96%
82%
Solution
96%
Let d be the original diameter.
Radius `="d"/2`
Thus, we have;
Original area `= π xx ("d"/2)`
`= (pi"a"^2)/4`
New diameter = 140% of d
`= (140/100xx"d")`
`= (7"d")/5`
Now,
New radius ` =(7"d")/5xx2`
`=(7"d")/10`
New area `= pixx((7"d")/10)^2`
`=(49π"a""^2)/10`
Increase in the area`=((49pi"a"^2)/10 - (pi"a"^2)/4)``
`=(24π"a"^2)/100`
`=(6pi"a"^2)/25 `
We have ;
Increase in the area`=((6pi"a"^2)/25xx4/(pi"a"^2)xx100)%`
= 96 %
APPEARS IN
RELATED QUESTIONS
A path of width 3.5 m runs around a semi-circular grassy plot whose perimeter is 72 m . Find the area of the path .
`("Use" pi= 22/7) `
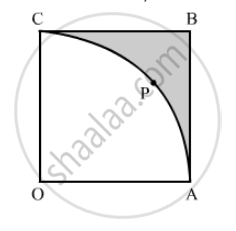
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
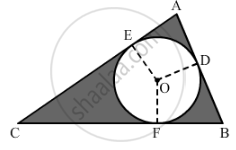
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
The area of a circle is 154 cm2. Its diameter is ____________.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
