Advertisements
Advertisements
Question
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
Solution
Side of the equilateral triangle = 12 m
Area of the equilateral triangle `= sqrt(3)/4xx("Side")^2`
`=sqrt(3)/4xx12xx12`
Length of the rope = 7 m
Area of the field the horse can graze is the area of the sector of radius 7 m .Also, the angle subtended at the centre is 60°
`=theta/360xxpi"r"^2`
`=60/360xx22/7xx(7)^2`
= 25.67 m2
Area of the field the horse cannot graze = Area of the equilateral triangle -- Area of the field the horse can graze
= 62.28 - 25.67 = 36.61 m2
APPEARS IN
RELATED QUESTIONS
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
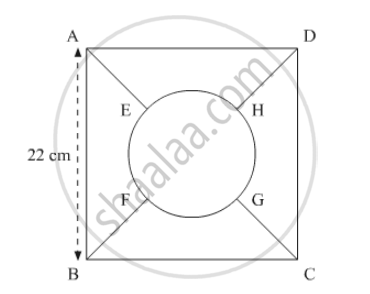
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
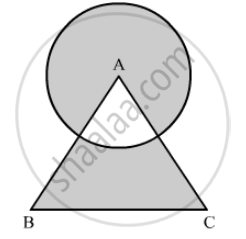
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The formula used to find the area of the circle is ________ sq.units
