Advertisements
Advertisements
प्रश्न
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
उत्तर
Let the breadth of the rectangular park be b.
∴ Length of the rectangular park`=l=2b`
Perimeter = 840 m
⇒`840=2(l+b)`
⇒`840=2(2b+b)`
⇒`840=2(3b)`
⇒`840=6b`
⇒b=140 m`
Thus, we have:
`l=2b`
=`2xx140`
=`280m`
Area `lxxb`
=`280xx140`
=`39200 m^2`
APPEARS IN
संबंधित प्रश्न
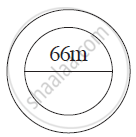
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

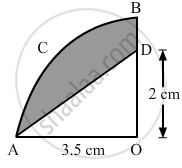
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
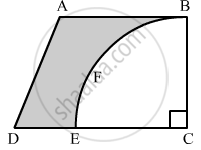
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
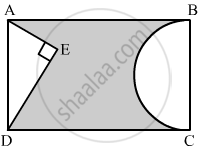
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
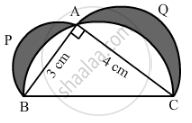
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
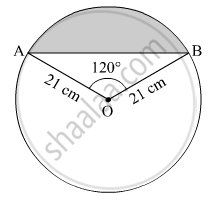
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
