Advertisements
Advertisements
प्रश्न
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
उत्तर
Area of the ring between two concentric circles = π(R2 - r2)
Where R and r are the radii of the outer and the inner circle respectively
Here there are three concentric circles,
the innermost of radius 6.3cm, the second of radius 8.4cm and the outermost of radius x cm (say)
⇒ π(8.42 - 6.32) = π(x2 - 8.42)
⇒ π(2 x 8.42 - 6.32) = πx2
⇒ (2 x 8.42 - 6.32) = πx2
⇒ (2 x 8.42 - 6.32) = x2
⇒ (141.12cm2 - 39.69cm2) = x2
⇒ x2 = 101.43cm2
⇒ x = 10.07cm.
APPEARS IN
संबंधित प्रश्न
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
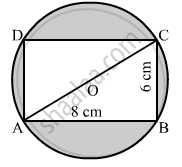
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
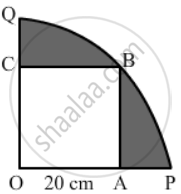
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
The radius of a circular wheel is 42 cm. Find the distance travelled by it in :
(i) 1 revolution ;
(ii) 50 revolutions ;
(iii) 200 revolutions ;
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
