Advertisements
Advertisements
प्रश्न
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
उत्तर

Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8 cm
⇒ `asqrt2 = 8`
⇒ `a = 4sqrt2` cm
Now, Diagonal of a square = Diameter of a circle
⇒ Diameter of circle = 8
⇒ Radius of circle = r = `"Diameter"/2`
⇒ `r = 8/2 = 4` cm
∴ Area of circle = `pir^2 = pi(4)^2`
= `16pi xx cm^2`
and Area of square = `a^2 = (4sqrt2)^2`
= 32 cm2
APPEARS IN
संबंधित प्रश्न
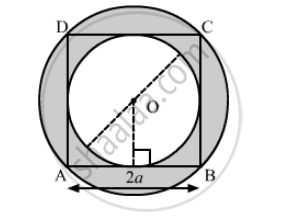
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

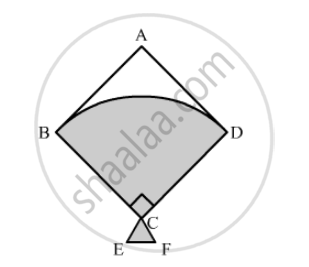
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
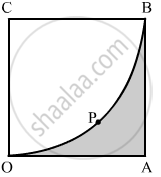
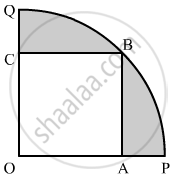
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
Find the area of a circle of radius 30 cm (use π = 3.14).
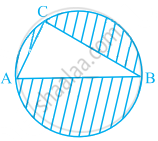
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).